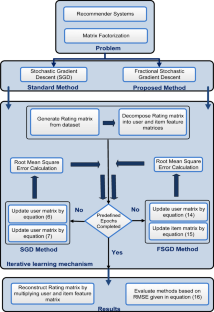
Fractional stochastic gradient descent for recommender systems

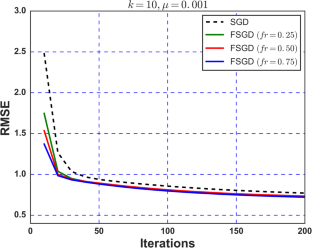
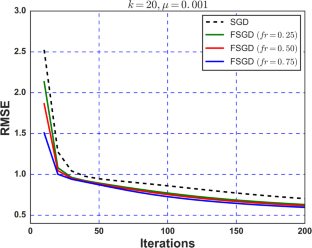
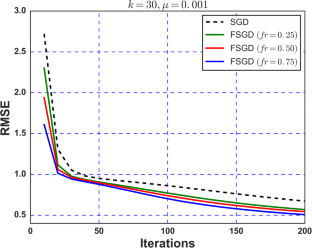
Recently, recommender systems are getting popular in the e-commerce industry for retrieving and recommending most relevant information about items for users from large amounts of data. Different stochastic gradient descent (SGD) based adaptive strategies have been proposed to make recommendations more precise and efficient. In this paper, we propose a fractional variant of the standard SGD, named as fractional stochastic gradient descent (FSGD), for recommender systems. We compare its convergence and estimated accuracy with standard SGD against a number of features with different learning rates and fractional orders. The performance of our proposed method is evaluated using the root mean square error (RMSE) as a quantitative evaluation measure. We examine that the proposed strategy is more accurate in terms of RMSE than the standard SGD for all values of fractional orders and different numbers of features. The contribution of fractional calculus has not been explored yet to solve the recommender systems problem; therefore, we exploit FSGD for solving this problem. The results show that our proposed method performs significantly well in terms of estimated accuracy and convergence as compared to the standard SGD.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save
Springer+ Basic
€32.70 /Month
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Buy Now
Price includes VAT (France)
Instant access to the full article PDF.
Rent this article via DeepDyve
Similar content being viewed by others

Design of normalized fractional SGD computing paradigm for recommender systems
Article 21 October 2019
MISGD: Moving-Information-Based Stochastic Gradient Descent Paradigm for Personalized Fuzzy Recommender Systems
Article 18 September 2021
RP-SWSGD: Design of sliding window stochastic gradient descent method with user’s ratings pattern for recommender systems
Article 11 October 2023
Explore related subjects
References
- Adomavicius, G., & Tuzhilin, A. (2005). Toward the next generation of recommender systems: A survey of the state- of-the-art and possible extensions. IEEE Transactions on Knowledge and Data Engineering, 17(6), 734–749. ArticleGoogle Scholar
- Aggarwal, C. C. (2016). An Introduction to Recommender Systems. In Recommender Systems (pp. 1–28). Springer International Publishing. https://doi.org/10.1007/978-3-319-29659-3_1.
- Aggarwal, C. C., & Parthasarathy, S. (2001). Mining massively incomplete data sets by conceptual reconstruction. In Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 227–232). ACM.
- Aslam, M. S., & Raja, M. A. Z. (2015). A new adaptive strategy to improve online secondary path modeling in active noise control systems using fractional signal processing approach. Signal Processing, 107, 433–443. ArticleGoogle Scholar
- Aslam, M. S., Chaudhary, N. I., & Raja, M. A. Z. (2017). A sliding-window approximation-based fractional adaptive strategy for Hammerstein nonlinear ARMAX systems. Nonlinear Dynamics, 87(1), 519–533. ArticleGoogle Scholar
- Badri, V., & Tavazoei, M. S. (2016). Some analytical results on tuning fractional-order [proportional–integral] controllers for fractional-order systems. IEEE Transactions on Control Systems Technology, 24(3), 1059–1066. ArticleGoogle Scholar
- Baskonus, H. M., & Bulut, H. (2015). On the numerical solutions of some fractional ordinary differential equations by fractional Adams-Bashforth-Moulton method. Open Mathematics, 13(1).
- Baskonus, H. M., Mekkaoui, T., Hammouch, Z., & Bulut, H. (2015). Active control of a chaotic fractional order economic system. Entropy, 17(8), 5771–5783. ArticleGoogle Scholar
- Bell, R. M., & Koren, Y. (2007, October). Scalable collaborative filtering with jointly derived neighborhood interpolation weights. In Data Mining, 2007. ICDM 2007. Seventh IEEE International Conference on (pp. 43–52). IEEE.
- Bobadilla, J., Ortega, F., Hernando, A., & Gutiérrez, A. (2013). Recommender systems survey. Knowledge-Based Systems, 46, 109–132. ArticleGoogle Scholar
- Bouzeriba, A., Boulkroune, A., & Bouden, T. (2016). Projective synchronization of two different fractional-order chaotic systems via adaptive fuzzy control. Neural Computing and Applications, 27(5), 1349–1360. ArticleGoogle Scholar
- Bulut, H., Baskonus, H. M., & Pandir, Y. (2013). The modified trial equation method for fractional wave equation and time fractional generalized Burgers equation. In Abstract and Applied Analysis (Vol. 2013). Hindawi Publishing Corporation.
- Chaudhary, N. I., Raja, M. A. Z., & Khan, A. U. R. (2015). Design of modified fractional adaptive strategies for Hammerstein nonlinear control autoregressive systems. Nonlinear Dynamics, 82(4), 1811–1830. ArticleGoogle Scholar
- Chaudhary, N. I., Zubair, S., & Raja, M. A. Z. (2017a). A new computing approach for power signal modeling using fractional adaptive algorithms. ISA Transactions, 68, 189–202. ArticleGoogle Scholar
- Chaudhary, N. I., Aslam, M. S., & Raja, M. A. Z. (2017b). Modified Volterra LMS algorithm to fractional order for identification of Hammerstein non-linear system. IET Signal Processing, 11(8), 975–985. ArticleGoogle Scholar
- Chaudhary, N. I., Ahmed, M., Khan, Z. A., Zubair, S., Raja, M. A. Z., & Dedovic, N. (2018a). Design of normalized fractional adaptive algorithms for parameter estimation of control autoregressive autoregressive systems. Applied Mathematical Modelling, 55, 698–715. ArticleGoogle Scholar
- Chaudhary, N. I., Manzar, M. A., & Raja, M. A. Z. (2018b). Fractional Volterra LMS algorithm with application to Hammerstein control autoregressive model identification. Neural Computing and Applications, 1–14.
- Chen, D., Chen, Y., & Sheng, H. (2010). Fractional variational optical flow model for motion estimation. In The 4th IFAC Workshop Fractional Differentiation and Its Application, Badajoz, Spain, Oct (pp. 18–20).
- Chen, D., Chen, Y., & Xue, D. (2015). Fractional-order total variation image denoising based on proximity algorithm. Applied Mathematics and Computation, 257, 537–545. ArticleGoogle Scholar
- Chen, D., Sun, S., Zhang, C., Chen, Y., & Xue, D. (2013). Fractional-order TV-L2 model for image denoising. Central European Journal of Physics, 11(10), 1414–1422. Google Scholar
- Chen, P. L., Tsai, C. T., Chen, Y. N., Chou, K. C., Li, C. L., Tsai, C. H., … & Yu, S. H. (2011). A linear ensemble of individual and blended models for music rating prediction. In Proceedings of the 2011 International Conference on KDD Cup 2011-Volume 18 (pp. 21–60). JMLR. org.
- Chin, W. S., Zhuang, Y., Juan, Y. C., & Lin, C. J. (2015). A fast parallel stochastic gradient method for matrix factorization in shared memory systems. ACM Transactions on Intelligent Systems and Technology (TIST), 6(1), 2. Google Scholar
- Elwakil, A. S. (2010). Fractional-order circuits and systems: An emerging interdisciplinary research area. IEEE Circuits and Systems Magazine, 10(4), 40–50. ArticleGoogle Scholar
- Funk, S. (2006). Netflix update: Try this at home. URLhttp://sifter.org/simon/journal/20061211.html.
- Gemulla, R., Nijkamp, E., Haas, P. J., & Sismanis, Y. (2011). Large-scale matrix factorization with distributed stochastic gradient descent. In Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 69–77). ACM.
- Geravanchizadeh, M., & Ghalami Osgouei, S. (2014). Speech enhancement by modified convex combination of fractional adaptive filtering. Iranian Journal of Electrical and Electronic Engineering, 10(4), 256–266. Google Scholar
- Harper, F. M., & Konstan, J. A. (2015). The movielens datasets: History and context. ACM Transactions on Interactive Intelligent Systems, 5(4). https://doi.org/10.1145/2827872.
- He, C., Parra, D., & Verbert, K. (2016). Interactive recommender systems: A survey of the state of the art and future research challenges and opportunities. Expert Systems with Applications, 56, 9–27. ArticleGoogle Scholar
- Heimbach, I., Gottschlich, J., & Hinz, O. (2015). The value of user’s Facebook profile data for product recommendation generation. Electronic Markets, 25(2), 125–138. ArticleGoogle Scholar
- Hofmann, T. (2004). Latent semantic models for collaborative filtering. ACM Transactions on Information Systems (TOIS), 22(1), 89–115. ArticleGoogle Scholar
- Jalab, H. A., Ibrahim, R. W., & Ahmed, A. (2017). Image denoising algorithm based on the convolution of fractional Tsallis entropy with the Riesz fractional derivative. Neural Computing and Applications, 1–7.
- Kawai, M., & Nogami, S. (2016). A Hybrid Recommender System of Collaborative and Content Based Filtering. International Information Institute (Tokyo). Information, 6B(19), 2177. Google Scholar
- Köhler, S., Wöhner, T., & Peters, R. (2016). The impact of consumer preferences on the accuracy of collaborative filtering recommender systems. Electronic Markets, 26(4), 369–379. ArticleGoogle Scholar
- Koren, Y. (2008). Factorization meets the neighborhood: a multifaceted collaborative filtering model. In Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 426–434). ACM.
- Koren, Y., Bell, R., & Volinsky, C. (2009). Matrix factorization techniques for recommender systems. Computer, 42(8), 42–49. ArticleGoogle Scholar
- Kurucz, M., Benczúr, A. A., & Csalogány, K. (2007). Methods for large scale SVD with missing values. In Proceedings of KDD cup and workshop (Vol. 12, pp. 31–38).
- Little, R. J., & Rubin, D. B. (2002). Bayes and multiple imputation. Statistical Analysis with Missing Data, Second Edition, 200–220.
- Lu, J., Wu, D., Mao, M., Wang, W., & Zhang, G. (2015). Recommender system application developments: a survey. Decision Support Systems, 74, 12–32. ArticleGoogle Scholar
- Luo, X., Xia, Y., & Zhu, Q. (2012). Incremental collaborative filtering recommender based on regularized matrix factorization. Knowledge-Based Systems, 27, 271–280. ArticleGoogle Scholar
- Luo, X., Xia, Y., & Zhu, Q. (2013). Applying the learning rate adaptation to the matrix factorization based collaborative filtering. Knowledge-Based Systems, 37, 154–164. ArticleGoogle Scholar
- Machado, J. T. (2015). Fractional order description of DNA. Applied Mathematical Modelling, 39(14), 4095–4102. ArticleGoogle Scholar
- Machado, J. T., Kiryakova, V., & Mainardi, F. (2011). Recent history of fractional calculus. Communications in Nonlinear Science and Numerical Simulation, 16(3), 1140–1153. ArticleGoogle Scholar
- Malek, H., Dadras, S., & Chen, Y. (2016). Fractional order ESR modeling of electrolytic capacitor and fractional order failure prediction with application to predictive maintenance. IET Power Electron, 9(16081613.16).
- Mnih, A., & Salakhutdinov, R. R. (2008). Probabilistic matrix factorization. In Advances in Neural Information Processing Systems (pp. 1257–1264).
- Ortigueira, M. D. (2011). Fractional calculus for scientists and engineers. Lecture Notes in Electrical Engineering (84), Springer Science & Business Media. https://doi.org/10.1007/978-94-007-0747-4.
- Ortigueira, M. D., & Machado, J. T. (2006). Fractional calculus applications in signals and systems. Signal Processing, 86(10), 2503–3094.
- Ortigueira, M. D., Ionescu, C. M., Machado, J. T., & Trujillo, J. J. (2015). Fractional signal processing and applications. Signal Processing, 107, 197. ArticleGoogle Scholar
- Pahnehkolaei, S. M. A., Alfi, A., & Machado, J. T. (2017c). Chaos suppression in fractional systems using adaptive fractional state feedback control. Chaos, Solitons & Fractals, 103, 488–503.
- Pahnehkolaei, S. M. A., Alfi, A., & Machado, J. T. (2017a). Dynamic stability analysis of fractional order leaky integrator echo state neural networks. Communications in Nonlinear Science and Numerical Simulation, 47, 328–337. ArticleGoogle Scholar
- Pahnehkolaei, S. M. A., Alfi, A., & Machado, J. T. (2017b). Uniform stability of Fractional Order Leaky Integrator Echo State Neural Network with multiple time delays. Information Sciences, 418, 703–716. ArticleGoogle Scholar
- Paterek, A. (2007). Improving regularized singular value decomposition for collaborative filtering. In Proceedings of KDD cup and workshop (Vol. 2007, pp. 5–8).
- Pazzani, M. J., & Billsus, D. (2007). Content-based recommendation systems (pp. 325–341). Springer Berlin Heidelberg: The adaptive web. Google Scholar
- Psychalinos, C., Elwakil, A. S., Radwan, A. G., & Biswas, K. (2016). Guest editorial: fractional-order circuits and systems: theory, design, and applications. Circuits, Systems, and Signal Processing, 35(6), 1807–1813. ArticleGoogle Scholar
- Pu, Y. F., Yi, Z., & Zhou, J. L. (2017). Fractional hopfield neural networks: Fractional dynamic associative recurrent neural networks. IEEE Transactions on Neural Networks and Learning Systems, 28(10), 2319–2333.
- Raja, M. A. Z., & Chaudhary, N. I. (2014). Adaptive strategies for parameter estimation of Box–Jenkins systems. IET Signal Processing, 8(9), 968–980. ArticleGoogle Scholar
- Raja, M. A. Z., & Chaudhary, N. I. (2015). Two-stage fractional least mean square identification algorithm for parameter estimation of CARMA systems. Signal Processing, 107, 327–339. ArticleGoogle Scholar
- Rennie, J. D., & Srebro, N. (2005). Fast maximum margin matrix factorization for collaborative prediction. In Proceedings of the 22nd international conference on Machine learning (pp. 713–719). ACM.
- Rostami, M., & Haeri, M. (2015). Undamped oscillations in fractional-order Duffing oscillator. Signal Processing, 107, 361–367. ArticleGoogle Scholar
- Sabatier, J., Agrawal, O.M., & Machado, J.A.T. (2007) Advances in fractional calculus. 4(9). Springer Dordrecht. BookGoogle Scholar
- Safarinejadian, B., Asad, M., & Sadeghi, M. S. (2016). Simultaneous state estimation and parameter identification in linear fractional order systems using coloured measurement noise. International Journal of Control, 89(11), 2277–2296. ArticleGoogle Scholar
- Safarinejadian, B., Asad, M., & Torabi Jahromi, A. (2014). A Hierarchical Identification Method for SISO Fractional-order State-space Systems. The Modares Journal of Electrical Engineering, 13(4), 17–28. Google Scholar
- Salter, J., & Antonopoulos, N. (2006). CinemaScreen recommender agent: combining collaborative and content-based filtering. IEEE Intelligent Systems, 21(1), 35–41. ArticleGoogle Scholar
- Sarwar, B., Karypis, G., Konstan, J., & Riedl, J. (2000). Application of dimensionality reduction in recommender system-a case study (No. TR-00-043). Minnesota Univ Minneapolis Dept of Computer Science. Accession Number: ADA439541. http://www.dtic.mil/dtic/tr/fulltext/u2/a439541.pdf.
- Schafer, J. B., Frankowski, D., Herlocker, J., & Sen, S. (2007). Collaborative filtering recommender systems. In The adaptive web (pp. 291–324). Springer Berlin Heidelberg.
- Srebro, N., Rennie, J., & Jaakkola, T. S. (2005). Maximum-margin matrix factorization. In Advances in Neural Lnformation Processing Systems, 17, (pp. 1329–1336).
- Takács, G., Pilászy, I., Németh, B., & Tikk, D. (2009). Scalable collaborative filtering approaches for large recommender systems. Journal of Machine Learning Research, 10(Mar), 623–656. Google Scholar
- Wang, Z., Yu, N., & Wang, J. (2016) Collaborative filtering recommendation algorithm based on matrix factorization and user nearest neighbors. In: Zhang L., Song X., Wu Y. (Eds.), Theory, Methodology, Tools and Applications for Modeling and Simulation of Complex Systems. AsiaSim 2016, SCS AutumnSim 2016. Communications in Computer and Information Science, Vol. 643. Springer, Singapore. https://doi.org/10.1007/978-981-10-2663-8_21.
- Wu, G. C., Baleanu, D., & Lin, Z. X. (2016). Image encryption technique based on fractional chaotic time series. Journal of Vibration and Control, 22(8), 2092–2099. ArticleGoogle Scholar
- Yu, H. F., Hsieh, C. J., Si, S., & Dhillon, I. (2012). Scalable coordinate descent approaches to parallel matrix factorization for recommender systems. In Data Mining (ICDM), 2012 I.E. 12th International Conference on (pp. 765–774). IEEE.
- Yu, H. F., Hsieh, C. J., Si, S., & Dhillon, I. S. (2014). Parallel matrix factorization for recommender systems. Knowledge and Information Systems, 41(3), 793–819. ArticleGoogle Scholar
- Zhou, Y., Wilkinson, D., Schreiber, R., & Pan, R. (2008). Large-scale parallel collaborative filtering for the netflix prize. In International Conference on Algorithmic Applications in Management (pp. 337–348). Springer Berlin Heidelberg.
- Zubair, S., Chaudhary, N. I., Khan, Z. A., & Wang, W. (2018). Momentum fractional LMS for power signal parameter estimation. Signal Processing, 142, 441–449. ArticleGoogle Scholar
Author information
Authors and Affiliations
- Department of Electrical Engineering, International Islamic University, Islamabad, 44000, Pakistan Zeshan Aslam Khan, Naveed Ishtiaq Chaudhary & Syed Zubair
- Zeshan Aslam Khan








